From my previous article on circles, we have learnt about how to calculate the Pi, circumference and diameter of circles.
It is also in order that we work out the area of any circle.
The area of a circle uses the formula , 𝛑r squared. But how did this come about? Since we know about the others, shall we find that of the area.
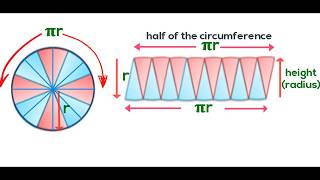
The first step is to draw a circle and draw straight lines across it (diameters) to divide the circle into equal portions. With the divisions we can have 4 equal parts (quarters), then eighths, sixteenths and so on.
The puzzle pieces formed from the circle can be merged together to form a rectangle. What we can realise from the arrangements of the portions of the circles is that every time the circle is further divided into smaller puzzle pieces and rearranged horizontally, the shape becomes even more rectangular. The circle can be further divided into several equal smaller parts and rearranged to get a perfect rectangle.
So when the circle eventually becomes a complete rectangle, the area of the circle will be equal to the area of the rectangle: length (base) x width (height).
As we arrange the pieces horizontally, we can observe that the pieces have the same heights; they form the radius of the circle.
The height of the rectangle is therefore the same as the radius. Radius then replaces height (in the formula).
Further on in the rearrangement, the puzzle pieces are put together alternatively, so that the apex (tip) of one, faces up and that of another faces down … going on in that pattern. As such, with 16 pieces for instance, 8 pieces will have their tips facing down and 8 pieces face up.
The rectangle now formed has its length (base) as the sum of widths of half of the pieces. This is half of circumference (if put back to form the circle). The full circumference (2𝛑r) is the sum of base/width of all of the pieces (16 pieces in this case).
Thus the length of the circle is the same as half of the circumference; becoming 𝛑r. This will be the same regardless of how many parts the circle is divided into.
So if the area of a rectangle = Length (𝛑r) x width (radius)
Then the area of a circle = 𝛑r x r = 𝛑r squared
The video below shows the explanation of 3 examples of how to calculate the area of circles with the diameter or radius given.